My Log
[ADsP #9] 데이터 분석 2장 - 통계 분석 (1) 본문
* 시작하기에 앞서 본 게시물에 포함된 내용은 한국데이터산업진흥원에서 발행한 [데이터 분석 전문가 가이드, 2019년 2월 8일
개정]에 근거한 것임을 밝힙니다.
1. 통계학 개론
가. 통계학이란?
- 자료로부터 유용한 정보를 이끌어 내는 학문 (자료의 수집, 정리, 해석하는 방법 등을 포함)
- 일기예보, 경제통계, 사회조사 분석통계, 실험결과 분석통계 등 다양한 형태
나. 통계 분석이란?
- 특정한 집단이나 불확실한 현상을 대상으로 자료를 수집 → 대상 집단에 대한 정보를 구함 → 적절한 통계 분석 방법을
이용한 의사결정(통계적 추론) 과정을 말함
- 통계적 추론에는 대상 집단의 특정값을 추측하는 추정 / 가설 설정 후 채택여부를 결정하는 가설검정 / 미래에 대한 예측이
있다.
다. 모집단
- 알고자 하는 정보의 대상
- 모집단을 구성하는 개체를 추출단위 혹은 원소라고 함
- 모집단에 대해 조사하는 방법
1) 총조사
- 모든 개체를 조사하는 방법, 많은 비용과 시간이 소요되므로 특별한 경우를 제외하고는 실시되지 않음
2) 표본조사
- 모집단의 일부분(표본)만 조사하여 모집단에 대해 추론
- 표본추출 방법에 따라 분석결과의 해석에 큰 차이가 발생할 수 있으므로,
모집단의 정의/표본의 크기/조사방법/조사기간/표본추출 방법을 명확하게 밝히거나 확인해야 한다.
- 표본추출 방법
가) 단순랜덤 추출법 : 말 그대로 랜덤추출
나) 계통 추출법 : K개의 표본을 추출할 때, 모집단을 K개의 구간으로 나눈 뒤 각 구간에서 하나를 랜덤 추출
다) 집락 추출법 : 모집단이 몇 개의 집락(cluster)으로 구성되어 있을 때, 집락을 랜덤 선택한 뒤 그 안에서 표본 추출
라) 층화 추출법 : 모집단이 이질적인 원소들로 구성되어 있을 때, 각 계층을 고루 대표할 수 있도록 계층별로 랜덤추출
라. 자료의 종류
1) 질적자료 : 대상이 속하는 집단을 분류하는 명목척도 / 서열관계나 선호도를 관측하는 순서척도
2) 양적자료 : 온도, 지수 등 속성의 양을 측정하는 구간척도 / 무게, 나이 등 숫자로 관측되는 일반적인 비율척도
마. 확률
- 확률 : 특정 사건이 일어날 가능성의 척도
- 표본공간 : 나타날 수 있는 모든 결과들의 집합
- 사건 : 표본공간의 부분집합
- 근원사건 : 한 개의 원소로만 이루어진 사건
- 배반사건 : 교집합이 공집합인 사건들
- 조건부 확률 : 특정 사건 A가 일어났다는 가정하의 사건 B의 확률
- 독립 : 사건 A가 일어났는지 여부와 상관없이 사건 B의 확률이 동일하면 서로 독립이라고 함
바. 확률변수와 확률분포
- 확률변수 : 정의역이 표본공간이고 치역이 실수값인 함수
1) 이산형 확률변수
- 사건의 확률을 각 이산점에서의 확률의 크기로 나타내는 확률질량함수로 표현
(예) 베르누이 확률분포, 이항분포, 기하분포, 다항분포, 포아송분포 등
2) 연속형 확률변수
- 사건의 확률을 함수의 면적으로 표현하는 확률밀도함수로 표현
- 면적으로 표현되므로 한 점에서의 확률은 0이다.
(예) 균일분포, 정규분포, 지수분포 등
사. 추정
- 통계적 추론은 추정과 가설검정으로 나눌 수 있는데, 그 중에서도 추정은 점추정과 구간추정으로 나뉜다.
1) 점추정
- 가장 참값이라고 여겨지는 하나의 모수의 값을 택하는 것 (모수가 특정한 값일 것이라고 추정)
- 사실상 추정이 얼마나 정확한가를 판단하기가 불가능
- 대표적인 예로 모평균과 모분산을 추정하기 위한 추정량인 표본평균과 표본분산이 있다.
2) 구간추정
- 점추정의 정확성을 보완하는 방법
- 일정한 크기의 신뢰수준(90%, 95%, 99% 등)으로 모수가 특정한 구간(신뢰구간)에 있을 것이라고 선언하는 것
- 신뢰수준 95%의 의미
: 모집단에서 동일한 방법으로 확률표본을 무한히 추출하여 신뢰구간을 구하면, 그 중에서 95%의 신뢰구간이 미지의 모수를
포함한다는 의미 (cf. 주어진 한 개의 신뢰구간이 미지의 모수를 포함할 확률이 95%라는 것과 구분해야 함)
아. 가설검정
- 모집단에 대한 귀무가설(H0)과 대립가설(H1)을 설정한 뒤, 표본관찰 또는 실험을 통해 하나를 선택하는 과정
1) 귀무가설(H0) : 대립가설과 반대의 증거를 찾기 위해 정한 가설
2) 대립가설(H1) : 증명하고 싶은 가설
- 귀무가설이 옳다는 전제하에서 관측된 검정통계량의 값보다 더 대립가설을 지지하는 값이 나타날 확률을 구하여
가설의 채택여부를 결정한다.
- p-value
* 귀무가설이 옳다는 가정하에 얻은 통계량이 귀무가설을 얼마나 지지하는 지를 나타낸 확률
** p-값이 작을수록 귀무가설을 기각할 가능성이 높아진다.
*** p-값이 유의수준(α)보다 작으면 귀무가설을 기각한다.
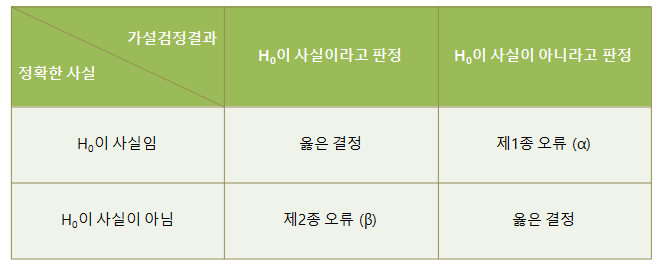
- 가설검정의 오류
* 제1종 오류와 제2종 오류는 상충관계가 있음
** 제1종 오류의 확률을 0.1, 0.05, 0.01 등으로 고정시킨 뒤, 제2종 오류가 최소가 되도록 기각역을 설정한다.
*** 기각역이란, 귀무가설을 기각하는 통계량의 영역을 말한다.
* 가설검정에 관한 이해가 부족하여 다른 블로그의 설명을 통해 공부하였으며, 아래 블로그를 참고하시면 쉽게 이해하실 수
있습니다.
1. https://blog.naver.com/choodonggeun/221188315171
세상에서 가장 쉽게 설명하는 귀무가설 대립가설 #H0 H1 #영가설 연구가설
자 이번시간에는 어떤 분의 요청으로 인해 귀무가설과 대립가설을 설명하고자 한다. (통계학 전공자가 아니...
blog.naver.com
2. https://blog.naver.com/choodonggeun/221181595852
세상에서 가장 쉽게 설명하는 p-value(유의확률) #유의확률 #p value #유의확률p #p값
비전공자로서 통계를 처음 공부하면서 모르는 용어들이 많았다. 책을 봐도 무슨 소리인지 모르겠는 말들이 ...
blog.naver.com
3. https://blog.naver.com/mini7000/221423290639
경영 통계 필기 (확률변수, 표본분포, p값, 귀무가설, 대립가설, 분산분석, 회귀분석, 카이제곱점검, bayes' theorem, poisson distribution)
<확률변수>-이산확률변수 -> 이항분포-연속확률변수 -> 정규분포 [모집단 -> 표본분...
blog.naver.com
자. 모수 검정
- 모집단의 모수에 대한 검정에는 모수적 방법과 비모수적 방법이 있다.
1) 모수적 검정
- 모집단의 분포에 대한 가정을 하고, 그 가정 하에서 검정통계량과 검정통계량의 분포를 유도해 검정을 실시하는 방법
- 가설의 설정 : 가정된 분포의 모수(모평균, 모분산 등)에 대한 가설 설정
- 검정 실시 : 관측된 자료를 이용해 표본평균, 표본분산 등을 구하여 검정 실시
2) 비모수적 검정
- 모집단의 분포에 대해 아무 제약을 가하지 않고 검정을 실시하는 검정 방법
- 관측 자료가 특정분포를 따른다고 가정할 수 없는 경우에 이용
- 가설의 설정 : 가정된 분포가 없으므로, 단지 '분포의 형태'가 동일한지 여부에 대해 가설 설정
- 검정 실시 : 관측값의 순위나 관측값 차이의 부호 등을 이용해 검정 실시
(예) 부호검정, 순위합검정, 부호순위합검정, U검정, 런검정, 순위상관계수 등
2. 기초 통계 분석
가. 기술통계
- 기술통계란 자료를 요약하는 기초적 통계를 의미한다.
- 분석에 앞서 데이터의 통계적 수치를 계산해봄으로써, 데이터에 대한 대략적인 이해와 분석의 통찰력을 얻기에 유리하다.
- R에서는 head(data), summary(data), mean(data$column), median(data$column), var(data$column),
max(data$column), min(data$column) 등의 함수로 기초통계량을 구해 확인한다.
나. 회귀 분석
1) 회귀 분석의 개념
- 회귀분석이란 하나나 그 이상의 변수들이 또 다른 변수에 미치는 영향에 대해 추론할 수 있는 통계기법이다.
* 반응변수(종속변수) : 영향을 받는 변수, 보통 y로 표기
* 설명변수(독립변수) : 영향을 주는 변수, 보통 x, x1, x2 등으로 표기
가) 단순회귀분석
- 회귀모형 중에서 가장 단순한 모형
- 한 개의 독립변수와 하나의 종속변수로 이루어짐
- 회귀계수의 추정치는 보통 제곱오차를 최소로 하는 값으로 구함
나) 다중회귀분석
- 단순회귀모형이 종속변수의 변동을 설명하는데 충분하지 않다는 점을 보완
- 두 개 이상의 독립변수를 사용하여 종속변수의 변화를 설명
- 단순/다중 회귀분석을 통해 적합한 모형을 찾은 후에는 모형이 적절한지 확인해야 함
ⅰ 모형이 통계적으로 유의미한가?
˙ F-통계량의 p-값이 0.05보다 작은지 확인
ⅱ 회귀계수들이 유의미한가?
˙회귀계수들의 p-값이 0.05보다 작은지 확인
ⅲ 모형이 얼마나 설명력을 갖는가?
˙결정계수를 확인
2) R에서의 회귀분석 수행 예제
가) 단순선형회귀분석
> lm ( y~x, data=데이터명 )
Call :
lm(formula = y ~ x, data = 데이터명)
Coefficients :
(Intercept) x
2.131 3.018
- 회귀방정식 y = 2.131 + 3.018x 로 추정
나) 다중선형회귀분석
> lm ( y~u+v+w, data=데이터명 )
Call :
lm(formula = y ~ u + v + w, data = 데이터명)
Coefficients :
(Intercept) u v w
3.203 0.1482 1.9752 -3.0081
- 회귀방정식 y = 3.203 + 0.1482u + 1.9752v - 3.0081w 로 추정
다) 모형의 적절성 여부 확인
> m <- lm ( y~u+v+w, data = 데이터명 )
> summary(m)
- summary 함수를 통해 F-통계량의 p-값, 결정계수, 회귀계수의 p-값을 확인하여 모형의 적절성 여부를 판단한다.
- 추가로 plot(m) 함수를 통해 회귀식의 잔차도를 확인하여 선형성을 파악한다.
3) 최적회귀방정식 선택 (설명변수의 선택)
- 반응변수 y에 영향을 미칠 수 있는 가능한 모든 설명변수를 가지고 있을 때, y의 변화를 설명하기 위한 설명변수를 어떻게
선택할지 고려해야 한다.
- 변수 선택에는 두 가지 원칙을 따른다. (이율배반적 원칙으로 상황에 적절한 변수를 선택해야 함)
* y에 영향을 미칠 수 있는 모든 설명변수 x들을 참여시킨다.
* x가 많아질수록 관리가 힘들기에, 가능한 범위 내에서 적은 수의 설명변수를 포함시킨다.
가) 모든 가능한 조합의 회귀분석
- 모든 가능한 독립변수들의 조합에 대한 회귀모형을 고려해 가장 적합한 회귀모형을 선택
나) 단계적 변수선택
ㄱ. 전진선택법
- 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
- 후보가 되는 설명변수 중 가장 설명을 잘하는 변수가 유의하지 않을 때의 모형을 선택
ㄴ. 후진제거법
- 독립변수 후보 모두를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거
- 더 이상 유의하지 않은 변수가 없을 때의 모형을 선택
ㄷ. 단계별방법
- 전진선택법에 의해 변수를 추가하면서, 기존 변수의 중요도가 약화되면 제거하는 등 단계별로 추가 또는 제거
- 더 이상 추가 또는 제거되는 변수가 없을 때의 모형을 선택
4) R에서의 단계적 변수선택 예제
가) 전진선택법
> step( lm(y~1, dfrm), scope=list(lower=~1, upper=~u+v+w), direction="forward" )
나) 후진제거법
> step( lm(y~u+v+w, dfrm), direction="backward" )
다) 단계별방법
> step( lm(y~1, dfrm), scope=list(lower=~1, upper=~u+v+w), direction="both" )
'자격증 기록 > ADsP(데이터분석 준전문가)' 카테고리의 다른 글
| [ADsP #11] 데이터 분석 3장 - 정형 데이터 마이닝(1) (0) | 2019.08.23 |
|---|---|
| [ADsP #10] 데이터 분석 2장 - 통계 분석 (2) (0) | 2019.08.22 |
| [ADsP #8] 데이터 분석 1장 - R 기초와 데이터마트(2) (0) | 2019.08.12 |
| [ADsP #7] 데이터 분석 1장 - R 기초와 데이터마트(1) (0) | 2019.08.11 |
| [ADsP #6] 데이터 분석 기획 2장 - 분석 마스터 플랜 (0) | 2019.08.05 |



